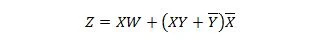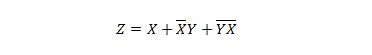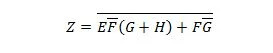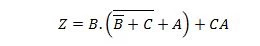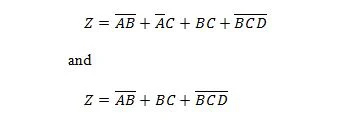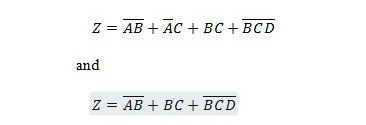Kapitel 2: Boolean algebra og dens relaterede computerkomponenter
2.1 Grundlæggende booleske operatører
Antag, at jeg (forfatteren) er høj, og du (læseren) er høj. Hvis nogen spørger dig, om vi begge er høje, ville du sige 'Ja' (sandt). Hvis han spørger, om vi begge er korte, vil du sige 'Nej' (falsk). Hvis du er lav, og jeg er høj, og han spørger dig, om enten du eller jeg er høj, vil dit svar være 'Ja' (sandt). Hvis han spørger, om både du og jeg er høje, ville du ikke have et svar. Du kan fortsætte med at sige, at det sidste spørgsmål ikke skal stilles, eller at spørgsmålet ikke har et svar. Nå, jeg vil have dig (læseren) til at vide, at i dag, under visse omstændigheder, bør spørgsmålet stilles.
I biologi er en person enten høj eller lav. Det er de 'miljømæssige' forhold, der gør, at personen har en middelhøjde. En videnskabsmand, George Boole, definerede et sæt svar eller regler for denne slags spørgsmål. Vi lærer disse regler i dette afsnit af online karrierekurset (kapitel). Disse regler bruges i dag inden for databehandling, programmering, elektronik og telekommunikation. Uden disse regler ville du faktisk ikke have en computer, som det er almindeligt i dag; du ville ikke også have programmering, som det er almindeligt i dag.
Sandt eller falsk
Et simpelt menneskeligt sprogudsagn er enten sandt eller falsk i sig selv. Hvis jeg siger, 'Jeg er høj', er det enten sandt eller falsk. Hvis jeg siger, 'du er høj', er det enten sandt eller falsk. Hvis jeg er høj, og du er lav, og spørgsmålet stilles, om både du og jeg er høje, skal der i boolesk logik gives et svar på sandt eller falsk. Hvilken af disse to skal gives? Boole svarede ikke rigtig på dette spørgsmål. Han kom simpelthen med et sæt regler, som vi skulle følge. Den gode nyhed er, at når du følger disse regler i deres rette sammenhæng, har du ingen uklarhed. Takket være disse regler har vi computere og programmering i dag. Reglerne er givet til dig nu. Reglerne kan ikke rigtigt forklares; du accepterer dem bare. Reglerne er under tre overskrifter: OG, ELLER og IKKE.
OG
Spørgsmålet kan stilles, om både du OG mig er høje. Min højde og din højde kombineres derefter af OG-regelsættet. Dette er OG-reglerne, der skal følges:
falsk OG falsk = falsk
falsk OG sand = falsk
sand OG falsk = falsk
sand OG sand = sand
Lad nu høj være sand og kort være falsk. Det betyder, at hvis jeg er lav OG du er lav, så er du og jeg korte. Hvis jeg er lav OG du er høj, er du og mig lave; det er det boolske svar, som du skal acceptere. Hvis jeg er høj OG du er lav, er både du og jeg lave. Hvis jeg er høj OG du er høj, er du og mig høje. Alt dette er OG booleske regler, som du (læseren) bare skal acceptere.
ELLER
Spørgsmålet kan stilles, om du ELLER mig er høj. Min højde og din højde kombineres derefter af OR-regelsættet. Disse OR-regler skal følges:
falsk ELLER falsk = falsk
falsk ELLER sand = sand
sand ELLER falsk = sand
sand ELLER sand = sand
Igen, lad høj være sand og kort være falsk. Det betyder, at hvis jeg er lav ELLER du er lav, er du ELLER mig kort. Hvis jeg er lav ELLER du er høj, er du eller mig høj. Hvis jeg er høj ELLER du er lav, er du ELLER mig høj. Hvis jeg er høj ELLER du er høj, er du eller mig høj. Alle disse er booleske regler, som du skal acceptere.
IKKE
Nu, i boolsk logik, eksisterer der kun to tilstande (mulige svar). Det vil sige, at hvis du IKKE er høj, er du lav. Hvis du IKKE er lav, er du høj; intet andet. Dette er IKKE-reglerne, der skal følges:
IKKE falsk = sand
IKKE sandt = falsk
Antag, at du har en snor (eller fjeder), som du kan forlænge (trække). Mens strengen er i sin naturlige tilstand, hvis jeg siger 'IKKE kort', ville du forlænge den; det er fortolkningen. Mens strengen er forlænget, hvis jeg siger 'IKKE lang', ville du tillade den at trække sig sammen; det er fortolkningen.
Du skal huske alle de givne regler i deres forskellige kategorier.
Mere end to operander
I et computersprog kaldes AND, OR og NOT hver for en operator. For NOT-operatoren behøver du kun én operand (værdi til en operator) for at få et svar. For AND- eller OR-operatorerne kan du have mere end to operander. De foregående tilfælde viser to operander for AND og OR. Du kan have tre operander for OG som følger:
falsk OG falsk OG falsk = falsk
falsk OG falsk OG sand = falsk
Det er to linjer; hver har to OG-operatorer. Der er faktisk ni linjer, når operanderne er tre. Med AND-operatoren er kun den sidste linje (niende linje) lig med sand; alle de foregående linjer er falske. Bemærk, at med to operander for AND, er kun den sidste linje stadig sand; alle de foregående tre linjer er falske. Når operanderne er fire, er der 16 linjer, og kun den sidste linje er sand for AND-operatoren.
Mønstret for OG og mønsteret for ELLER er forskellige. Med tre operander for to OR-operatorer er der også ni linjer, og kun den første linje, denne gang, er falsk. Den anden til den niende linje er sand. Bemærk, at med to operander for OR, er kun den første linje stadig sand; alle de resterende tre linjer er falske. Når operanderne er fire for OR, er der også 16 linjer.
NOT-operatoren behandler kun én operand. IKKE falsk er sand og IKKE sand er falsk.
2.2 To operand sandhedstabel og deres elektroniske komponenter
I matematik er der et emne kaldet algebra. En lille del af det blev set i forrige kapitel. Der er en slags algebra kaldet boolsk algebra. I boolsk algebra identificeres sand ved grundtonen to cifret, som er 1, og falsk er identificeret med basis to cifferet, som er 0.
Komponenterne til den interne computerenhed er elektroniske komponenter. Systemenheden i computersystemet har digitale elektroniske komponenter. AND-operationen udføres af en lille elektronisk komponent kaldet AND-porten. OR-operationen udføres af den lille elektroniske komponent kaldet OR-porten. NOT-operationen udføres af den lille elektroniske komponent kaldet NOT-porten. For mange af disse porte kan være i en IC-chip (Integrated Circuit).
OG Sandhedsbordet og dets port
Følgende tabel giver OG-sandhedstabellen og dens OG-port (lille kredsløb) symbol:
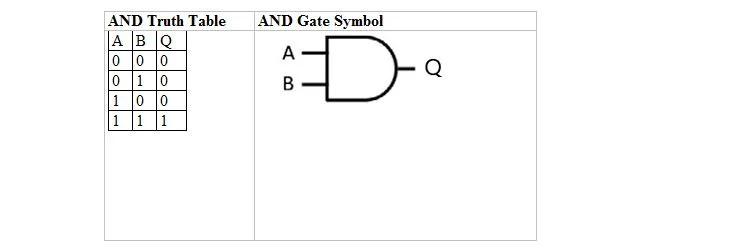
For både AND-sandhedstabellen og dens port er A såvel som B to inputvariable. Q er outputvariablen. A er enten 1 eller 0. B er enten 1 eller 0. Q er enten 1 eller 0. OG-sandhedstabellen med 1'er og 0'er er den samme som den tidligere sand/falsk OG sandhedslayout (tabel). OG-ligningen er:
A . B = Q
hvor prikken (.) betyder OG (Boolsk). Prikken kan udelades for at have AB = Q, hvilket betyder det samme (OG).
Bemærk: Bittene for A og B i de fire rækker, som par, er de første fire tal i basis to, der begynder fra 0 (eller 00), dvs. 00, 01, 10, 11.
Følgende tabel giver OR-sandhedstabellen og dens OR-gate (lille kredsløb) symbol:
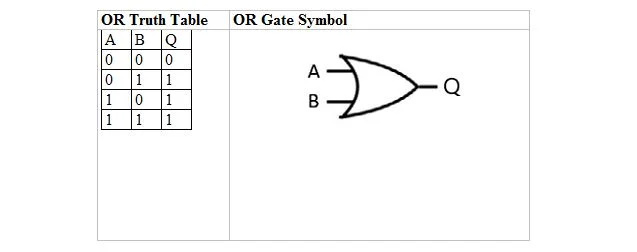
For både OR-sandhedstabellen og dens port er A såvel som B to inputvariable. Q er outputvariablen. ELLER-sandhedstabellen med 1'er og 0'er er den samme som den tidligere sand/falsk ELLER sandhedslayout (tabel).
OR-ligningen er:
A + B = Q
Hvor + her betyder Boolean ELLER og ikke addition. Ligningen læses som 'A eller B lig med Q'.
Følgende tabel giver NOT sandhedstabellen og dens NOT gate (lille kredsløb) symbol:
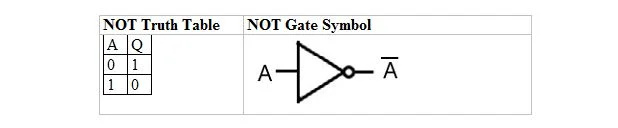
NOT-sandhedstabellen eller NOT-porten har kun én indgang og én udgang. Når indgangen er 0, er udgangen 1. Når indgangen er 1, er udgangen 0. NOT-porten laver en slags inversion. Outputvariablen er den samme som inputvariablen, men med en streg (overstreget). NOT-sandhedstabellen med 1'er og 0'er er den samme som den tidligere sand/falsk ELLER sandhedslayout (tabel).
NOT-ligningen er:
A = Q
Hvor Q = A og stregen over A betyder her komplement. Komplementet af 0 er 1 og komplementet af 1 er 0. NOT-porten er også kendt som INVERTERENDE port.
Disse er de grundlæggende (eller rod) sandhedstabeller og deres porte (små kredsløb) i digital elektronik (med boolsk algebra). De andre tre sandhedstabeller, der er givet i den følgende illustration, og deres porte er for nemheds skyld og er baseret på de foregående tre sandhedstabeller.
Der er en sandhedstabel og -port, der er afledt af OG-sandhedstabellen og -porten. De kaldes NAND (for IKKE OG) sandhedstabellen og den tilsvarende NAND-port. NAND-sandhedstabellen og dens NAND-port er:
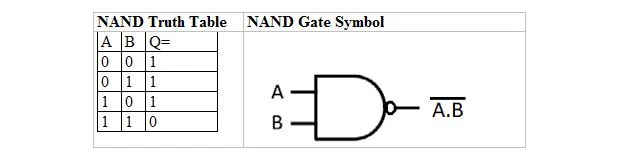
For at få NAND-sandhedstabellen skal du gå til outputtet af OG-sandhedstabellen og erstatte hvert ciffer med dets komplement. Komplementet af 0 er 1 og komplementet af 1 er 0. NAND-porten er ligesom OG-porten, men har en lille cirkel før udgangslinjen. NAND-ligningen er:
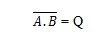
Hvor betyder komplementet af resultatet af 'A' OG 'B'. Baren (over-line) er repræsenteret i porten af den lille cirkel. Bemærk, at prikken mellem A og B kan udelades.
Der er en anden sandhedstabel og -port, der er afledt af OR-sandhedstabellen og -porten. De kaldes NOR (for IKKE ELLER) sandhedstabellen og den tilsvarende NOR-port. NOR-sandhedstabellen og dens NOR-port er:
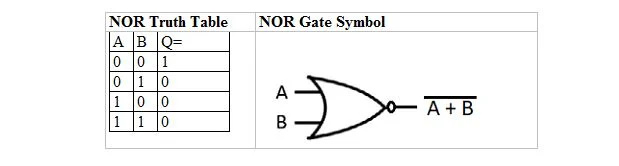
For at opnå NOR-sandhedstabellen skal du gå til outputtet af OR-sandhedstabellen og erstatte hvert ciffer med dets komplement. Komplementet af 0 er 1 og komplementet af 1 er 0. NOR-porten er ligesom OR-porten, men har en lille cirkel før udgangslinjen. NOR-ligningen er:
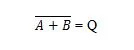
Hvor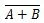 
betyder komplementet af resultatet af 'A' ELLER 'B'. Baren (overlinien) er repræsenteret i porten af den lille cirkel.
Eksklusiv ELLER (XOR)
Sandhedstabellen for OR-porten er:
På almindeligt engelsk er det ikke klart, om den sidste række af 1 ELLER 1 skal give 1 eller 0. Så i boolsk algebra er der to slags ELLER-sandhedstabeller og to tilsvarende porte. Med den normale ELLER giver den sidste række af 1 ELLER 1 1. Den anden type ELLER er eksklusiv-ELLER (XOR), hvor de første tre rækker er de samme som de første tre rækker af normal ELLER (inklusive output). Men for den fjerde og sidste række giver 1 ELLER 1 0.
Følgende tabel giver XOR-sandhedstabellen og dens XOR-gate (lille kredsløb) symbol:
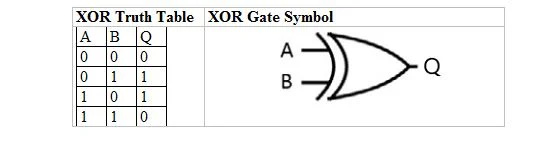
For både XOR-sandhedstabellen og dens port er 'A' såvel som 'B' to inputvariabler. 'Q' er outputvariablen.
XOR-ligningen er:
A ⊕ B = Q
Hvor ⊕ her betyder Boolean XOR.
Den normale ELLER betyder den ene eller begge. Eksklusiv ELLER betyder strengt enten og ikke begge dele.
2.3 Booleske postulater
Postulater er antagelser baseret på hvilke der drages visse konklusioner. Der er ti boolske postulater, der er rodfæstet fra OG-, ELLER- og IKKE-ligningerne (sandhedstabellerne). Disse ligninger kaldes også funktioner. De grundlæggende funktioner kopieres som følger:
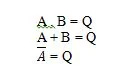
Disse er de grundlæggende funktioner (ligninger) i boolsk algebra. Følgende andre tre (funktions) ligninger er ikke fundamentale funktioner:
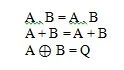
Selvom den sidste funktion her er ejendommelig, betragtes den ikke som en grundlæggende funktion.
De boolske postulater er som følger:
Fra OG-funktion
1) 0 . 0 = 0
tyve. 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1
Fra OR-funktion
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1
Fra NOT-funktion
9) 0 = 1
10) 1 = 0
Bemærk: Disse postulater er blot linjerne i OG-, ELLER- og IKKE-sandhedstabellerne, der udtrykkes på en uafhængig måde. Læseren bør huske de givne postulater.
2.4 Booleske egenskaber
En ejendom er en lignende karakteristik af noget. Boolske egenskaber er ligninger, der er afledt af de boolske postulater. I dette afsnit er egenskaberne blot givet uden deres afledninger og derefter brugt bagefter. Der er femogtyve af ejendommene, der er grupperet under ti overskrifter som følger:
Egenskaber for AND-funktionen
Ejendom 1:
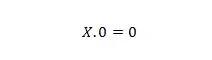
Hvor X kan være 1 eller 0. Det betyder, at uanset hvad X er, er resultatet altid 0.
Bemærk: En variabel må ikke nødvendigvis være A eller B eller C eller D. En variabel kan være W eller X eller Y eller Z eller et hvilket som helst andet bogstav.
Ejendom 2:
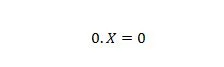
Hvor X kan være 1 eller 0. Bemærk, at forskellen mellem egenskab 1 og egenskab 2 er, at på venstre side af lighedstegnet for begge ligninger, er positionerne af X og 0 byttet om.
Ejendom 3:
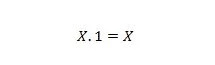
Hvis X er 0, så er 0. 1 = 0. Hvis X er 1, så er 1. 1 = 1.
Ejendom 4:
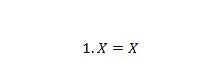
Hvis X er 0, så er 1. 0 = 0. Hvis X er 1, så er 1. 1 = 1. Bemærk, at forskellen mellem egenskab 3 og egenskab 4 er, at på venstre side af begge ligninger er positionerne af X og 1 er ombyttet.
Egenskaber for OR-funktionen
Ejendom 5:
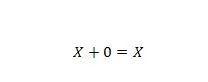
Hvor X kan være 1 eller 0. Det betyder, at hvis X er 0, er resultatet 0. Hvis X er 1, er resultatet 1.
Ejendom 6:
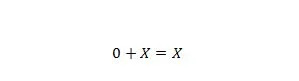
Hvor X kan være 1 eller 0. Bemærk, at forskellen mellem egenskab 5 og egenskab 6 er, at på venstre side af begge ligninger, er positionerne af X og 0 ombyttet.
Ejendom 7:
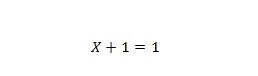
Hvis X er 0, så er 0 + 1 = 1. Hvis X er 1, så er 1 + 1 = 1.
Ejendom 8:
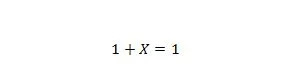
Hvis X er 0, så er 1 + 0 = 1. Hvis X er 1, så er 1 + 1 = 1. Bemærk, at forskellen mellem egenskab 7 og egenskab 8 er, at på venstre side af begge ligninger er positionerne af X og 1 er ombyttet.
Egenskaber vedrørende kombinationen af en variabel med sig selv eller dens komplement
Ejendom 9: 
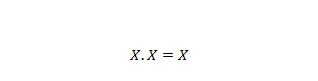
Det vil sige: hvis X er 0, så 0 . 0 = 0. Hvis X er 1, så 1 . 1 = 1.
Ejendom 10:
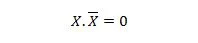
Det vil sige: hvis X er 0, så er 0. 1 = 0. Hvis X er 1, så er 1. 0 = 0.
For på hinanden følgende variable bliver denne egenskab:
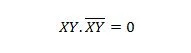
Ejendom 11:
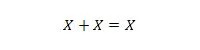
Det vil sige: hvis X er 0, så er 0 + 0 = 0. Hvis X er 1, så er 1 + 1 = 1 (fra normal ELLER).
Ejendom 12:
Det vil sige: hvis X er 0, så er 0 + 1 = 1. Hvis X = 1, så er 1 + 0 = 1.
Det vil sige: hvis X er 0, så er 0 + 1 = 1. Hvis X = 1, så er 1 + 0 = 1.
Dobbelt komplementering
Ejendom 13:
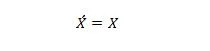
Når X på venstre side er 0, bliver X på højre side 0. Når X på højre side er 1, bliver X på venstre side 1. Med andre ord, dobbelte komplementer giver den oprindelige værdi tilbage.
Kommutativ lov
Ejendom 14:
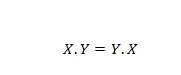
Det betyder, at det er ligegyldigt at udveksle den første og den anden operand for AND-operatoren på venstre side af lighedstegnet; svaret er stadig det samme efter udvekslingen i venstre side har fundet sted. Denne ligning kan skrives med prikkerne udeladt som: XY = YX.
Ejendom 15:
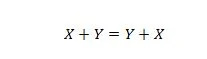
Forklaringen her er den samme som i det foregående OG, men det er for OR-operatoren.
Fordelingslov
Ejendom 16:
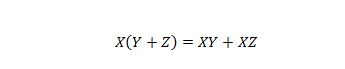
Her er der tre variabler: X, Y og Z. Hver variabel kan være enten 1 eller 0. På venstre side af lighedssymbolet betyder parenteserne først at evaluere, hvad der står i dem. Så er AND resultatet med X. Højre side siger, at X OG Y sammen, ELLER X OG Z sammen, er det samme som venstre side. Bemærk, at prikoperatoren for AND er udeladt hele vejen igennem; og de sammenføjede variable betyder stadig OG.
Ejendom 17:
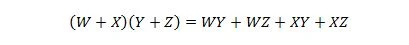
Denne egenskab er en udvidelse af ejendom 16 med den tilføjede variabel W.
Associativ ret
Ejendom 18:
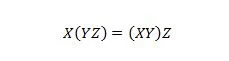
Brackets betyder først at vurdere, hvad der står i parentes. Så for udtrykket på venstre side, hvis Y med Z er ANDed først, og X er ANDed med resultatet, så er det endelige resultat på venstre side det samme som det endelige resultat til højre -hånd-side hvor X med Y er ANDed først før ANDing af resultatet med Z. Bemærk at prikkerne er udeladt i ligningen.
Ejendom 19:
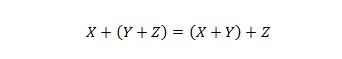
Denne egenskab er forklaret på samme måde som egenskab 18, men OR-operatoren er ansat i stedet for AND-operatoren. OR-operatoren + udelades aldrig fra et boolesk udtryk for enkelhedens skyld. På den anden side kan AND-operatoren udelades, og de to variable kan kombineres.
Absorption
Ejendom 20:
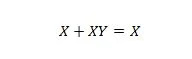
Med denne ligning, uanset hvad Y er, vil højre side altid være X (absorberet).
Ejendom 21:
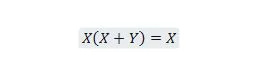
Også med denne ligning, uanset hvad Y er, vil højre side altid være X (absorberet). Denne ejendom 21 er den samme som med ejendom 20, som er:
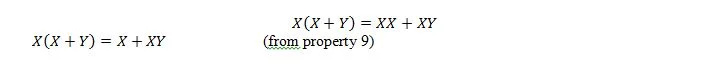
Her bruger vi fordelingsloven og det faktum, at X.X = X af ejendom 9.
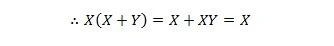
En identitet
Ejendom 22:
Det betyder, at for X + Y-udtrykket ændrer komplementet af X foran Y ikke udtrykket.
Ejendom 23:
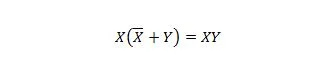
Dette betyder, at for XY-udtrykket ændrer komplementet af X ORed med Y i parentes, som udføres først, ikke XY-udtrykket.
DeMorgans lov
Ejendom 24:
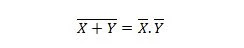
Dette betyder, at en NOR (NOT OR)-port har det samme resultat som at NOTE de to indgange før ANDing af dem.
Ejendom 25:
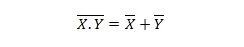
Dette betyder, at en NAND (NOT AND) gate har samme resultat som at NOTE de to inputs før ORing.
De medfølgende illustrationer er de 25 ejendomme. De kan bevises ved at erstatte alle de forskellige mulige værdier af 1'er og 0'er, i hvert udtryk på venstre side, for at se om udtrykket (eller resultatet) på højre side er opnået. Beviserne efterlades som en øvelse for læseren.
2.5 Forenkling af sammensatte udtryk
Følgende to funktioner er de samme:
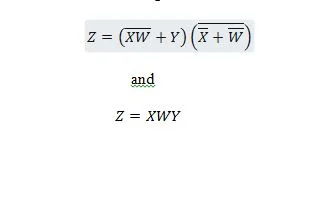
Z er output og X, W og Y er input. Den første har brug for en NAND-port, en OR-gate, en AND-gate, to IKKE-porte, en OR-gate og en NOR-port. Den anden behøver kun to OG-porte. Den første er en ligning med et sammensat udtryk på højre side, som er blevet forenklet (reduceret) til det enkelte højre udtryksudtryk for den anden ligning.
Forenkling eller reduktion fører til færre antal porte for at implementere den samme funktion som et kredsløb. Sådan et mindre kredsløb kan være en del af et integreret kredsløb (IC) eller være et selvstændigt kredsløb på overfladen af computerens bundkort.
Når en funktion (ligning) ankommer til designprocessen, skal der forenkles for at reducere antallet af porte og ende med et billigere kredsløb. Forenkling kræver anvendelse af en eller flere af de foregående 25 boolske egenskaber.
Eksempel 2.51:
Reducer ligningen:
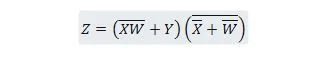
Bemærk: To parenteser ved siden af hinanden betyder, at parenteserne er ANDed (prikken mellem dem er eventuelt ikke skrevet).
Løsning:
For løsningerne er begrundelsen (årsagen) for hvert trin angivet til højre for trinnet i parentes. Læseren bør læse hvert trin og dets begrundelse. Læseren bør også henvise til de tidligere egenskaber, når han/hun læser funktionsreduktionstrinnene.
Eksempel 2.52:
Forenkle:
2.6 Minimumsum af produkter
Følgende to funktioner er de samme:
Begge højrehåndsudtryk af begge ligninger siges at være i Sum of Products (SP) form. Et udtrykkeligt udtryk siges at være i Sum of Product-formen, hvis det ikke har parentes. Det er indlysende, at den første funktion (ligning) har brug for flere porte end den anden funktion.
Det første højrehåndsudtryk kan stadig reduceres for at opnå den anden funktion. Det andet udtryk på højre side kan ikke forenkles yderligere og stadig udtrykkes som Sum of Products ('tilføjelse' af vilkår). Det andet udtryk på højre side kan egentlig ikke forenkles yderligere. Så det siges at være i formen Minimum Sum of Products (MSP).
Eksempel 2.61:
Bring den følgende funktion først til formen Sum of Products og derefter til formularen Minimum Sum of Products.
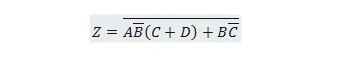
Løsning:
Når man løser problemer som dette, skal en eller flere af de foregående 25 egenskaber bruges som illustreret i denne løsning:
2.6 Minimumsum af produkter
Følgende to funktioner er de samme:
Begge højrehåndsudtryk af begge ligninger siges at være i Sum of Products (SP) form. Et udtrykkeligt udtryk siges at være i Sum of Product-formen, hvis det ikke har parentes. Det er indlysende, at den første funktion (ligning) har brug for flere porte end den anden funktion.
Det første højrehåndsudtryk kan stadig reduceres for at opnå den anden funktion. Det andet udtryk på højre side kan ikke forenkles yderligere og stadig udtrykkes som Sum of Products ('tilføjelse' af vilkår). Det andet udtryk på højre side kan egentlig ikke forenkles yderligere. Så det siges at være i formen Minimum Sum of Products (MSP).
Eksempel 2.61:
Bring den følgende funktion først til formen Sum of Products og derefter til formularen Minimum Sum of Products.
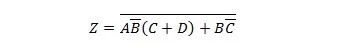
Løsning:
Når man løser problemer som dette, skal en eller flere af de foregående 25 egenskaber bruges som illustreret i denne løsning:
Dette sidste udtryk er i Sum of Products-form (SP), men ikke i Minimum Sum of Products-form (MSP). Første del af spørgsmålet er blevet besvaret. Løsningen til anden del er som følger:
Denne sidste forenklede funktion (ligning) er i MSP-form og har brug for mindre antal porte til implementering end dens tilsvarende SP-form. Husk: SP betyder Sum of Products, mens MSP betyder Minimum Sum of Products.
Eksempel 2.62:
Det følgende kredsløb har X-, Y- og W-indgangene, og Z er udgangen. Fremstil funktionen Sum of Products (SP) (tilsyneladende minimumsum af produkters funktion) for Z. Fremstil derefter den sande mere reducerede (minimerede) Sum of Products (MSP). Implementer derefter MSP-kredsløbet (tegn MSP-gating-netværket).
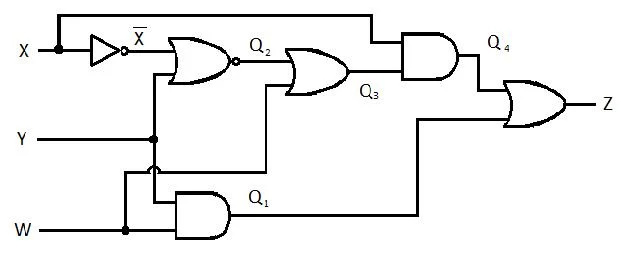
Fig. 2.61 Et portkredsløb
Løsning:
Før forenklingsprocessen starter, skal udtrykket for Z fås i form af X, Y og W. Se denne eksempelillustration fra diagrammet:
Dette er udtryk for Z i form af X, Y og W. Herefter kan forenklingen til tilsyneladende MSP finde sted. Tilsyneladende MSP er SP.
Denne sidste ligning (funktion) er i SP-form. Det er ikke sandt Minimum Sum of Products (endnu ikke MSP). Så reduktion (minimering) skal fortsætte.
Denne sidste ligning (funktion) er en sand minimumsum af produkter (MSP). Og minimumsummen af produkter (ægte minimering) portkredsløb er:
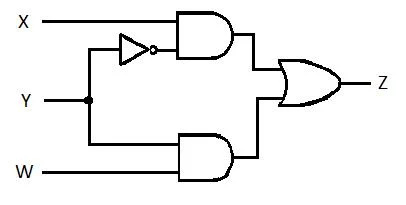
Fig. 2.62 MSP-portkredsløb
Kommentar
Ud fra analysen i dette afsnit kan det ses, at det ikke er klart, om Summen af Produkter er Minimumssummen af Produkter eller ej. SP er ikke særlig nyttig. Det er MSP, der er meget nyttigt. Der er en sikker måde at opnå MSP på; det er at bruge Karnaugh-kortet. Karnaugh Map er uden for rammerne af dette online karrierekursus.
2.7 Problemer
Læseren rådes til at løse alle problemerne i et kapitel, før de går videre til næste kapitel.
- Fremstil AND, OR og NOT sandhedstabellerne med deres tilsvarende porte.
- Skriv de ti boolske postulater ned i deres forskellige kategorier, og navngiv kategorierne.
- Uden forklaring, skriv de seksogtyve egenskaber af boolsk algebra ned i deres forskellige kategorier, navngiv kategorierne.
- Reducer ligningen ved at bruge de boolske egenskaber og citer de anvendte kategorier.
- Reducer ligningen ved at bruge de boolske egenskaber og citer de anvendte kategorier.
- Brug de booleske egenskaber og citer de anvendte kategorier, reducer følgende ligning – først til Sum of Products og derefter til Minimum Sum of Products:
- Brug de booleske egenskaber og citer de anvendte kategorier, reducer følgende ligning – først til Sum of Products og derefter til Minimum Sum of Products:
