Kapitel 3: Binære taloperationer i mikroprocessoren
3.1 Indledning
I en computer udføres aritmetiske operationer i 8 bit, 16 bit, 32 bit eller 64 bit. Et tal som 3 i binær er 11. Hvis operationen skal udføres i 8 bit, betragtes dette som 00000011; foran den med 0 nuller.
For et binært tal som 10000101 er den mest signifikante bit bit yderst til venstre. Det er 1 i dette tilfælde. Den mindst signifikante bit er den ekstreme bit til højre, som stadig er 1, for tallet. Den mest signifikante bit forkortes til MSB. Den mindst signifikante bit forkortes som LSB.
Det BInære cifre forkortes BIT og skrives ganske enkelt som bit. I tallet 10010011 er hver en eller nul lidt. En gruppe på fire bits kaldes en nibble. En gruppe på otte bit kaldes en byte. En byte består af to nibbles. Den lavere nibble er nibble for LSB og den højere nibble er nibble for MSB.
En gruppe på 8 bit, 16 bit, 32 bit eller 64 bit kaldes et ord, så længe den gruppe formidler information ud over blot at angive et tal. Gruppen kaldes for eksempel et ord, hvis det er en instruktion på lavt niveau i computeren. Der er også et ord på 24 bit, men det er ikke almindeligt brugt i dag.
Endianness refererer til den rækkefølge, hvori bytes danner et ord. Overvej det 24-bit ord – 100100001111010100100010. Dette ord består af tre bytes, som er:
10010000 11110101 00100010
Den mest betydningsfulde byte er den mest venstre byte. Når byten yderst til venstre er den mest signifikante byte, og byten yderst til højre er den mindst signifikante byte, omtales dette som den store endiske repræsentation af ordet. Little Endian-repræsentationen er det modsatte.
Computerens hukommelse er en række celler, og hver celle rummer en byte. Den første celle i computerens hukommelse er for byte 0, den anden er for byte 1, den tredje er for byte 2, og så videre. Med big endianness og for det foregående ord er den mest signifikante byte gemt i byte 0 celle, den midterste byte er gemt i byte 1 celle, og den mindst signifikante byte er gemt i byte 2 celle. Dette betyder, at der er mere signifikante byte i den nederste hukommelsescelle.
Det foregående 24-bit ord kan skrives i omvendt rækkefølge af bytes som følger:
00100010 11110101 10010000
Nu er den mindst signifikante byte yderst til venstre, og den mest signifikante byte er yderst til højre. Når byten yderst til venstre er den mindst signifikante byte, og byten yderst til højre er den mest signifikante byte, er det Little Endian-repræsentationen af ordet. Med lidt endianness og for det foregående ord, er den mindst signifikante byte gemt i byte 0 celle, den midterste byte er gemt i byte 1 celle, og den mest signifikante byte er gemt i byte 2 celle. Det betyder, at der er mindre signifikant byte i den nederste hukommelsescelle.
Endianness bruges ikke til bits i en byte. Det bruges heller ikke til nibbles i en byte. Det bruges kun til byte-rækkefølge.
Tallinjen
Et tal uden fortegn er et positivt tal. Positive tal er tal fra nul, der går opad. Negative tal findes også. Positive og negative tal kan præsenteres på en tallinje. Følgende tallinje viser de positive og negative hele tal (heltal) nær nul:
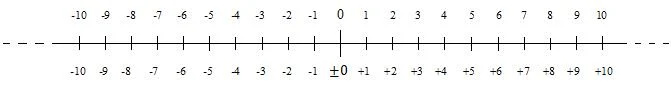
Negative tal falder fra nul og nedad (til venstre). I mange situationer betragtes nul som positivt. Det betragtes dog som negativt i nogle situationer. Derfor er der et plus- og minustegn foran nul, i den nederste nummerering, i diagrammet. Når et tal er positivt, kan dets fortegn udelades; dette er tilfældet for den øverste nummerering i diagrammet. Minustegnet foran et negativt tal udelades aldrig.
3.2 Tilføjelse af binære tal
I tilføjelsen:
A + B = S
A kaldes augend, B kaldes addend, og S kaldes summen.
Overvej følgende tilføjelse af to positive tal i basis to:

I grundtallet to er de eneste mulige cifre 0 og 1. Addition i grundtallet 2 svarer til addition i grundtallet ti, men to i grundtallet to er et-nul (10). Når summen af to bits i en kolonne er 10, skrives 0, og 1 føres til den umiddelbare venstre kolonne; skal lægges til summen af de to bits der. Når den samlede sum er tre, betyder det 11 i basis to. Den højre 1 ud af 11 skrives, og den venstre 1 bæres for at blive tilføjet til summen af de umiddelbare venstre kolonnebit. I begge tilfælde kaldes den 1, der bæres til venstre, bæreren.
Når man læser den forrige additionstabel fra højre, i anden kolonne (fra højre), er der en carry, som er resultatet af 1+1 = 10. I den tredje kolonne er der en carry, der er resultatet af 1+1+ carry af 1 = 11. I den fjerde kolonne er der en carry, som er resultatet af 0+1+ carry af 1 = 10. I den femte kolonne er der ingen carry, fordi summeringen er 0+0+ carry af 1 = 1. resten af søjlerne involverer ingen transport.
Kolonnetælling begynder fra højre ende. Med 16-bit addition kan der være en carry fra den ottende kolonne til den niende kolonne (bevæger sig til venstre). Følgende tabel illustrerer dette:

Aritmetiske og logiske operationer foregår i mikroprocessoren på computerens bundkort.
For en 8-bit word-computer kan carry ikke automatisk gå fra den ottende bit til den niende bit af hardware. Så for at tilføje to 16-bit grupper i en sådan computer, skal tilføjelsen udføres to gange i otte-otte bitpar. Bæret flyttes og udføres af softwaren (programmering).
For at tilføje to tal kan tallene først konverteres til deres tos komplementform (se nedenfor), før de tilføjes.
3.3 To-komplement og dets subtraktion af binære tal
På computerens bundkort er der hukommelsen, og der er mikroprocessoren og andre kredsløb. Hukommelsen er en serie af otte-bit celler. For en byte går hver bit ind i en celle. Mikroprocessoren har nogle få hukommelses-type placeringer. Disse placeringer af hukommelsestypen kaldes registre. Så i computeren kan grupper af bytes gemmes midlertidigt i hukommelsen eller i mikroprocessorens registre.
I ethvert af disse lager kan hver celle tage enten et 1 eller et 0, og intet andet. I livet er der positive og negative tal. Et positivt tal begynder med et plustegn (+), og et negativt tal begynder med et negativt fortegn (-). Når tegnet er udeladt, betragtes tallet som et positivt tal.
For at løse dette problem med at angive fortegnet for et tal i computeren, gemmes de hele tal i intervaller. Heltal er heltal. Hvis der bruges otte bit til at gemme rækken af mulige tal, bruges biten længst til venstre som fortegnsbit. Hvis tallet begynder med 0, er tallet et positivt tal. Hvis det begynder med 1, er tallet et negativt tal. Hvis der bruges seksten bit til at lagre rækken af mulige tal, bruges biten længst til venstre som fortegnsbit. Hvis tallet begynder med 0, er t tallet et positivt tal. Hvis det begynder med 1, er tallet et negativt tal. Numrene i denne formular kaldes signerede numre.
I praksis kan der være fortegnsnumre for 8 bit, 16 bit, 32 bit og 64 bit. Jo bredere antallet af bit bruges, jo større rækkevidde af mulige tal, der kan lagres.
Tos komplement heltal
Med to’s komplement er de positive tal de normale tælletal, bortset fra at cifferet længst til venstre er 0. For at opnå det tilsvarende negative tal for et givet positivt tal, skal du vende hver bit i tallet og lægge 1 til resultatet. Inverteringen eller komplementet af 0 er 1. Inverteringen eller komplementet af 1 er 0. Følgende tabeller viser nogle tos komplementtal i deres intervaller:
| Tabel 3.31 To's komplementer heltal i to bits |
|
|---|---|
| Binær | Decimal |
| 01 | +1 |
| 00 | +0 |
| elleve | -1 |
| 10 | -2 |
De positive binære tal er 00 og 01 (det vil sige nul og en). I stykket længst til venstre viser nul, at de er positive tal. 00 er lidt i midten af intervallet. For at opnå -1 findes inverteringen af tallet 01 til at være 10. Tilføjelse af 1 til dette (yderst til højre) giver 11.
Da der bruges to bit, er der kun én bit tilbage til at repræsentere tallene i området, som består af tallene +1, +0 og -1 svarende til 01, 00 og 11. Den første bit angiver tegnet. Det sker, at 10 for +2 ikke er blandt disse tre binære tal. 10 begynder med 1, hvilket betyder, at det skal være et negativt tal i to’s komplement. Så 10 er inkluderet i området, hvilket betyder -2.
Med to bit i to's komplement er antallet af alle de heltal (positive og negative), der kan repræsenteres, 2 2 = 4 og ikke 2 2 -1 = 3. Nuancen er resultatet af medtagelsen af det sidste negative tal, som er det negative af 2 nummer med – 1. I dette tilfælde -2 2-1 = -2 1 = -2. Der er ingen +2 i intervallet af tos komplementtal i 2 bit.
| Tabel 3.32 To's komplementære heltal i fire bits |
|
|---|---|
| Binær | Decimal |
| 0111 | +7 |
| 0110 | +6 |
| 0101 | +5 |
| 0100 | +4 |
| 0011 | +3 |
| 0010 | +2 |
| 0001 | +1 |
| 0000 | +0 |
| 1111 | -1 |
| 1110 | 1110 |
| 1101 | -3 |
| 1101 | -3 |
| 1100 | -4 |
| 1011 | -5 |
| 1010 | -6 |
| 1001 | 1001 |
| 1000 | -8 |
De positive binære tal er fra 0000 til 0111 (det vil sige fra nul til syv). I stykket længst til venstre viser nul, at de er positive tal. 0000 er noget midt i intervallet. For at opnå -1 findes inverteringen af tallet 0001 til at være 1110. Tilføjelse af 1 til dette (yderst til højre) giver 1111. For at opnå -2 findes inverteringen af 0010 at være 1101. Tilføjelse af 1 til dette ( fra yderst til højre) giver 1110. De andre negative binære tal som -3 til -7 bestemmes på samme måde.
Da der bruges fire bit, er der tre bit tilbage til at repræsentere tallene i området, som er +7, +6, +5, +4, +3, +2, +1, +0, -1, -2, - 3, -4, -5, -6 og -7 svarende til 0111, 0110, 0101, 0100, 0011, 0010, 0001, 0000, 1111, 1110, 1101, 1100, 1011, og 1011, 1.
De -8, der svarer til 1000, skal adresseres separat. Den første bit for alle disse tal angiver tegnet 0 for positive tal og 1 for negative tal. Det sker, at 1000 ikke er blandt disse fjorten binære tal. 1000 begynder med 1, hvilket betyder, at det skal være et negativt tal, hvad angår tos komplement. Så 1000 er inkluderet i intervallet, hvilket betyder -8.
Med fire bit i to's komplement er antallet af alle de heltal (positive og negative), der kan repræsenteres, 2 4 = 16 og ikke 2 4 – 1 = 15. Nuancen er resultatet af medtagelsen af det sidste negative tal, som er det negative af 2 nummerBredde – 1. I dette tilfælde -2 4 -1 = -2 3 = -8. Der er ingen +8 i rækken af tal.
Den tidligere analyse for to, fire og bredere bit i to's komplement kan anvendes på 8 bits, 16 bits, 32 bits og 64 bits brede binære tal.
Tos komplement ofrer den første (længst til venstre) bit for tegnet 0 for positivt tal og 1 for negativt tal. For den 'n' bit brede gruppe af bits er der 2 n samlede positive plus negative tal. Det ville være 2 n -1, var det ikke for det heldige sidste (mindste) negative tal inkluderet. Det højeste positive tal er +2 n-1 -1 og det mindste negative tal er -2 n-1 -1. Det ville være -2 n-1 -1, var det ikke for de heldige -2 n-1 inkluderet.
Subtrahering af tal i tos komplement
Ved subtraktion:
A – B = D
A kaldes minuend, B kaldes subtrahend, og D kaldes forskellen.
For at trække et positivt binært tal fra et andet positivt binært tal, skrives minuenden i tos komplement, og subtrahenden konverteres til dens negative tos komplementværdi. Så det matematiske udsagn bliver:
A+ – B = D
Med andre ord, i tos komplement subtraktion konverteres subtrahenden til et negativt tal og tilføjes derefter minuenden.
Eksempel 3.31:
Evaluer følgende decimaludtryk i to-komplement ved hjælp af fire bit:
6 – 4
Løsning:
Det binære tal for 6 er 110. I 4-bit to's komplement er det 0110. Det binære tal for +4 er 100. I 4-bit to's komplement er det 0100. 0100, som skal konverteres til negativ 4 i to'er komplement som følger: Komplementet eller inversionen af 0100 er 1011. Tilføjelse af 1 til dette fra den højre ende, som vi gjorde desuden, giver 1100. Så decimaludtrykket er:
6 – 4 som bliver:
0110 – 0100, dvs
0110 +(– 0100) = 0110 + 1100 udført som i det foregående tilføjelsesafsnit som:

Bemærk: 0110 +(– 0100) er det samme som 6 + – 4
Med to’s komplement subtraktion bliver enhver carry, efter den sidste kolonne mod venstre, i additionen, smidt væk. Når man trækker fra i decimal, er den matematiske sætning:
6 – 4 = 2
Hvis du gør det samme i to's komplement, er svaret 0010, hvilket er +2 i to's komplement binære optælling. Den foregående subtraktion trækker et mindre tal fra et større tal. I det følgende eksempel trækkes et større tal fra et mindre tal. Tabel 3.32 kan konsulteres for at se, om 0010 virkelig er to's komplement, hvilket svarer til +2.
Eksempel 3.32:
Evaluer følgende decimaludtryk i to-komplement med fire bit:
4 – 6
Løsning:
Det binære tal for 4 er 100. I 4-bit to-komplement er det 0100. Det binære tal for +6 er 110. I 4-bit to-komplement er det 0110. 0110 skal konverteres til negativt 6 i to-komplement som følger: Komplementet eller inversionen af 0110 er 1001. Tilføjelse af 1 til dette fra højre ende, som vi gjorde i den foregående tilføjelse, giver 1010. Så decimaludtrykket er:
4 – 6, som bliver:
0100 – 0110, dvs
0100 +(– 0110) = 0100 + 1010 udført som i det foregående tilføjelsesafsnit som:

Bemærk: 4+ – 6 er det samme som 0100 +(– 0110).
Med to’s komplement subtraktion bliver enhver carry, efter den sidste kolonne mod venstre, i additionen, smidt væk. Når man trækker fra i decimal, er den matematiske sætning:
4 – 6 = -2
Gør du det samme i to's komplement, er svaret 1110, hvilket er -2 i to's komplement binær tælling. Tabel 3.32 kan konsulteres for at se, om 1110 virkelig er to's komplement, hvilket svarer til -2.
3.4 Multiplikation af binære tal
I erklæringen:
A x B = P
A kaldes multiplikanten, B kaldes multiplikatoren, og P kaldes produktet. A x B-udtrykket betyder at tilføje A, B antal gange, når A og B er heltal (heltal).
Multiplikation i binær er det samme som multiplikation i decimal. Men i stedet for at gøre det i decimal, gøres det binært. Multiplikationen af decimaludtrykket på 42 x 10 udføres binært som følger, hvor 42 10 = 101010 2 og 10 10 = 1010 2 :
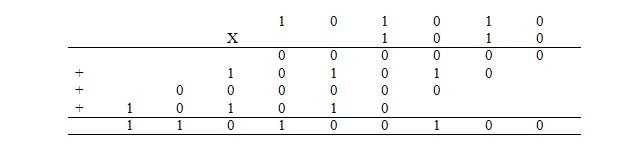
De 4 numre, der tilføjes, betegnes som delprodukter. Svaret er produktet. Tilsætningen af delprodukterne sker på samme måde som forklaret tidligere.
Multiplikationen kan også ses på følgende måde: I denne basis to multiplikation, hvis bit (cifret) i multiplikatoren er 1, er den mindst signifikante bit af dets partielle produkt den mindst signifikante bit af multiplikationen, som genskrives direkte under den; og resten af multiplikanets bits gentages til venstre. I denne basis to-multiplikation, hvis bit (cifre) i multiplikatoren er 0, består dens delprodukt af 0'er med den mindst signifikante bit på 0 direkte under sig. Antallet af alle nuller er antallet af bits i multiplikanet.
3.5 Division af binære tal
I erklæringen:
A ÷ B = Q
A kaldes Dividende, B kaldes Divisor, og P kaldes Quotient. Kvotienten kan være ledsaget af en rest. A ÷ B-udtrykket betyder, hvor mange gange B kan tilføjes for at give A eller være tæt på det, således at resten er 0 eller mindre end B.
Opdeling kan ske på mange måder. Inddelingen, der er vist her, er restaureringsinddelingen.
Gendannelse af division
Dette er den lange divisionsmetode, der læres i skolerne. Hvis 237 divideres med 6, er svaret 39 rest 3. De 237 10 i base 2 er 11101101 2 og 6 10 i base 2 er 110 2 . Den 39 10 i base 2 er 100111 2 og 3 10 i base 2 er 11 2 .
Altså 11101101 2 divideret med 110 2 giver 100111 2 resten 11 2 i base to. Med gendannelsesmetoden er de binære tal almindelige tal, og de er ikke nødvendigvis i tos komplement. Følgende struktur deler 11101101 2 med 110 2 at give 100111 2 resten 11 2 :

Subtraktion udføres almindeligt og ikke ved at bruge de tos komplement. Da dette er basis to, er et lån to og ikke ti. Deludbyttet er 10, 101, 1011, 1010 og 1001. 11 er resten. Da divisoren har tre cifre, sker opdelingen som udgangspunkt i grupper af tre cifre fra det givne udbytte. Kvotienten er det hele tal (heltal), og den er 100111 for dette problem. Kvotient- og restresultatet er som forventet.
3.6 Aritmetiske operationer med software og hardware
Computerens bundkort har et ur. Urets tikker kaldes pulser. Ved hver klokkepuls tages en eller flere beslutninger forskellige steder på bundkortet; og det har at gøre med programmering (software).
Inde i mikroprocessoren er der to slags kredsløb kaldet: Combinational Logic Circuits og Sequential Logic Circuits. Der er en anden slags kredsløb kaldet en multiplekser. Addition, multiplikation og division kan finde sted inden for et clock-interval ved hjælp af den kombinationslogik (kredsløb). Mens programmering (software) begår beslutning ved hver clock-impuls ved hjælp af de sekventielle logiske kredsløb og multipleksere.
Når subtraktion udføres ved hjælp af to's komplement, er mindst to clock-impulser nødvendige. Ved den første clock-impuls kanaliserer en multiplekser subtrahenden til et sæt IKKE-porte (én IKKE-port pr. ciffer). Ved den anden clock-impuls tilføjer kombinationslogikken 1 til outputtet fra NOT-portene og fortsætter med at tilføje den resulterende subtrahend og minuend. Al den tilføjelse kan finde sted inden for et urinterval.
Addition, multiplikation og division kan stadig være nede med programmering ved hjælp af sandhedstabellerne. Det er dog ikke dækket i dette online karrierekursus.
3.7 Logiske operationer i mikroprocessoren
AND, OR, XOR og Invert
OG
Følgende tabel illustrerer Bitwise OG. Dette betyder, at for to forskellige binære tal er de tilsvarende bits AND-behandlet baseret på AND-sandhedstabellen:
Flytning fra venstre mod højre, 1 OG 1 = 1; 0 OG 1 = 0; 0 OG 0 = 0; 1 OG 0 = 0; og så videre i overensstemmelse med OG-sandhedstabellen.
ELLER
Følgende tabel illustrerer Bitwise OR. Dette betyder, at for to forskellige binære tal, er de tilsvarende bits ORed baseret på OR-sandhedstabellen:

Flytning fra venstre mod højre, 1 ELLER 1 = 1; 0 ELLER 1 = 1; 0 ELLER 0 = 0; 1 ELLER 0 = 1; og så videre i overensstemmelse med OR-sandhedstabellen.
GRATIS
Følgende tabel illustrerer Bitwise exclusive-OR. Dette betyder, at for to forskellige binære tal XOR-behandles de tilsvarende bit baseret på XOR Truth-tabellen:

Flytning fra venstre mod højre, 1 XOR 1 = 0; 0 XOR 1 = 1; 0 XOR 0 = 0; 1 XOR 0 = 1; og så videre i overensstemmelse med XOR Truth Table.
Inverter (IKKE)
Følgende tabel illustrerer Bitwise NOT (inverter). Dette betyder, at for et binært tal, denne gang, er hver bit inverteret baseret på NOT Truth-tabellen:

Flytning fra venstre mod højre, IKKE 1 = 0; IKKE 0 = 1; IKKE 0 = 1; IKKE 1 = 0; og så videre i overensstemmelse med NOT Truth Table.
Skift til højre eller venstre
Skift til højre
Følgende binære tal forskydes 3 bitpositioner til højre, med nullerne indsat i de ledige bitpositioner til venstre:

Skiftet kan udføres for et, to, tre, fire osv. steder.
Skift til venstre
Følgende binære tal forskydes 3 bitpositioner til venstre, med nullerne indsat i de ledige bitpositioner til højre:

Skiftet kan udføres for et, to, tre, fire osv. steder.
Roterer til højre eller venstre
Rotation svarer til at skifte. Det gøres en smule ad gangen. Ved højredrejning falder de bits, der forlader den højre ende, ikke af som ved skift; de erstatter de ledige stykker til venstre, én efter én. Når man drejer til venstre, falder bitsene, der forlader den venstre ende, ikke af som ved skift; de erstatter de ledige stykker til højre, én efter én.
Drej til højre
Følgende binære tal roteres 3 bitpositioner til højre:

Rotationen kan udføres for et, to, tre, fire osv. steder.
Rorate til venstre
Følgende binære tal roteres 3 bitpositioner til venstre:

Rotationen kan udføres for et, to, tre, fire osv. steder.
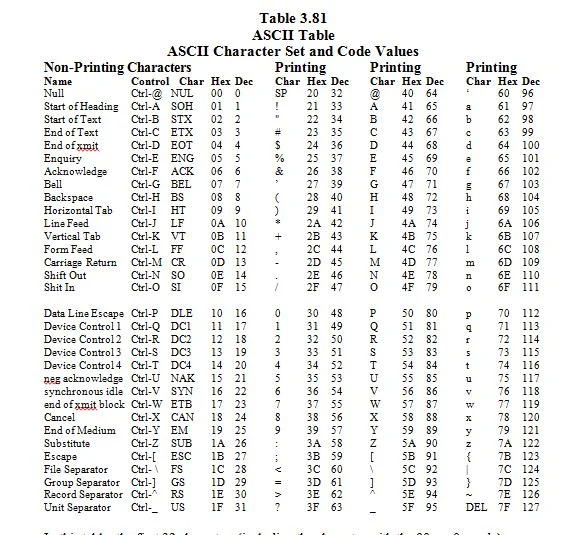
3.8 ASCII-tegnsæt og dets kodeværdier
ASCII står for 'American (U.S.A) Standard Code for Information Interchange'. Forestil dig et tastatur med 96 taster. Dette er et ideelt tastatur, hvor taster med store bogstaver er forskellige fra taster med små bogstaver. Hver anden tast repræsenterer et tegn, der findes på et engelsk (U.S.A) tastatur. Tegnene og koderne (tilsvarende tal for tegnene) er angivet i følgende:
I denne tabel er de første 32 tegn (inklusive tegnet med 00 16 = 0 10 kode) er ikke-udskrivende tegn. De er kontrolkarakterer. De ses ikke på skærmen (monitoren), hvor alt er lige. De har kun virkninger. Lad os diskutere mere om det senere.
Resten af tegnene er udskriftstegn; de ses på skærmen. Der er 128 ASCII-tegn. 2 7 = 128. 1.111.111 2 = 127 10 . De 7 i 2 7 betyder 7 bit.
Nu, 1111111 2 + 1 2 er det samme som:
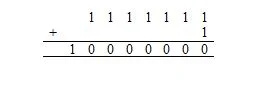
Her 10.000.000 2 = 128 10 . Der er 128 10 tegn i den foregående liste (tabel) over ASCII-tegn. Dette inkluderer null-tegnet, hvis kode i grundtallet seksten (hexadecimal) er 00, hvilket svarer til 0 i grundtallet ti.
Da der er 128 tegn i alt, giver 128 minus 32 ikke-udskrivende tegn 96 udskrivningstegn. I dette afsnit antages det, at der er et ideelt tastatur med 96 tegn, som kan udskrives. På dette ideelle tastatur er tasterne til de store engelske tegn forskellige fra tasterne til de små engelske tegn.
Hvert tegn på tastaturet er repræsenteret af et to-tal på 7 bit, som ikke er vist på listen. Det store bogstav i 'N' er for eksempel repræsenteret af de syv bit 1001110 i grundtal 2. For at konvertere 1001110 2 til base 16 skal du gå foran med 0 og gruppere resultatet i fire-bit undergrupper som følger:
| 0100 | 1110 | 2 = | 4 | E | 16
Det er 01001110 2 = 4E 16 . For at konvertere 4E 16 for at basere ti skal du gøre følgende:
4 x (16) 1 + E x (16) 0 = 4 x 16 + E x 1 = 4 x 16 + 14 x 1 = 64 + 14 = 78 10
Til højre for 'N' i listen (tabel) er det hexadecimale tal på 4E og decimaltallet på 78.
Som et andet eksempel er tegnet '[' repræsenteret af de syv bit 1011011 i base 2. For at konvertere 1011011 2 til base 16 skal du gå foran med 0 og gruppere resultatet i fire-bit undergrupper som følger:
| 0101 | 1011 | 2 = | 5 | B | 16
Det er 01011011 2 = 5B 16 . Gør følgende for at konvertere 5B16 til basis ti:
5 x (16) 1 + B x (16) 0 = 5 x 16 + B x 1 = 5 x 16 + 11 x 1 = 80 + 11 = 91 10
Til højre for '[' i listen (tabel) er det hexadecimale tal på 5B og decimaltallet på 91.
Som endnu et eksempel er tegnet for decimaltallet '5' repræsenteret af de syv bit 0110101 i base 2, og ikke 0000101 i basis 2. For at konvertere 0110101 2 til base 16 skal du gå foran med 0 og gruppere resultatet i fire-bit undergrupper som følger:
| 0011 | 0101 | 2 = | 5 | B | 16
Det er 00110101 2 = 35 16 . Gør følgende for at konvertere 3516 til basis ti:
3 x (16) 1 + 5 x (16) 0 = 3 x 16 + 5 x 1 = 3 x 16 + 5 x 1 = 48 + 5 = 53 10
Til højre for '5' i listen (tabel) er det hexadecimale tal på 35 og decimaltallet på 53.
Da computeren arbejder i bytes, sendes der otte bits til mikroprocessoren (bundkortet), når der trykkes på en tast på det ideelle tastatur. Det ideelle tastatur er en perifer enhed, som er adskilt fra computerens system (base) enhed. Den har et elektronisk kredsløb (IC), der skaber de syv bit og går forud for det med et nul, før det sendes gennem dets kabel til systemenhedens bundkort. Fra bundkortets input-port (input-kredsløb) går den til mikroprocessoren som også er på bundkortet. Fra mikroprocessoren går den til hukommelsen som også er monteret på bundkortet.
Så når 'N'-tasten på det ideelle tastatur trykkes, tages otte bit 01001110 til mikroprocessoren. Fra mikroprocessoren føres de til hukommelsen, hvor de forbliver på en hukommelsesplacering som en byte. Computerprogrammøren skal huske på, at de otte bits af 01001110 2 er det samme som 4E 16 hvilket er det samme som 78 10 .
Når der trykkes på '['-tasten på det ideelle tastatur, føres otte bit 01011011 til mikroprocessoren. Fra mikroprocessoren føres de til hukommelsen, hvor de forbliver på en hukommelsesplacering som en byte. Computerprogrammøren skal huske på, at de otte bits af 01011011 2 er det samme som 5B 16 hvilket er det samme som 91 10 .
Når '5'-tasten på det ideelle tastatur trykkes, som et tegn og ikke som et decimaltal, tages otte bit 00110101 til mikroprocessoren. Fra mikroprocessoren føres de til hukommelsen, hvor de forbliver på en hukommelsesplacering som en byte. Computerprogrammøren skal huske på, at de otte bits af 00110101 2 er det samme som 35 16 hvilket er det samme som 5310 10 .
Der er tidspunkter, hvor et program kører og venter på, at decimaltallet 5 indtastes i computeren. I denne situation, hvis der trykkes på '5'-tasten på det ideelle tastatur, tages stadig otte-bit-koden 00110101 til mikroprocessoren. Da det, der er nødvendigt, er decimaltallet på 5, og ikke '5'-tegnet, bruger et stykke kode (kort program) fra hukommelsen mikroprocessoren til at konvertere tegnkoden 00110101 i basis to til de tos komplementnummer 00000101 2 før du sender den til en hukommelsesplacering som en to-komplement-byte. Computerprogrammøren skal huske på, at 00000101 betyder 5 10 i base 2, og det er forskelligt fra kodenumrene på 00110101 2 , 35 16 og 53 10 hvilket betyder tegnet '5'. For at vise de tos komplementnummer på 00000101 i hukommelsen, skal et andet kort program konvertere 00000101 fra hukommelsen til 00110101. Det er 00110101, som er det samme som 35 16 hvilket er det samme som 53 10 der vises på skærmen (eller udskrives på et papir af printeren).
3.9 Floating Point Number Format
Et tal uden en decimaldel er et heltal. Tallet 36 er et heltal. 36.375 er ikke et heltal. Det er et decimaltal med en decimaldel. Decimaldelen af 0,375 er en brøkdel, der er mindre end 1.
36.375 fortolkes i decimalform som:
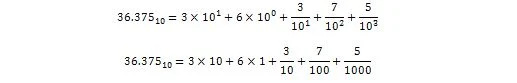
Nu:
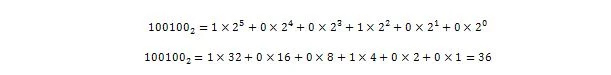
Altså 100100 2 = 3610, som er hele taldelen af 36,375 10 .
Nu:
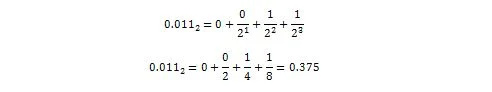
Altså 0,011 2 = 0,375 10 som er decimaltalsdelen af 36.375 10 .
∴ 36.375 10 = 100100,011 2
Sagt på en anden måde:
100100.011 2 = 36.375 10
Tal er repræsenteret i computeren i base 2 og ikke i base 10, hvor alt er lige. Da en celle i et register i mikroprocessoren eller en celle i hukommelsen kun kan tage 1 eller 0, er der ikke plads til at gemme et decimaltegn. Dette udgør et problem. Som opløsning er der IEEE-754 enkelt præcision 32-bit flydende komma-repræsentation og IEEE-754 dobbelt præcision 64-bit flydende komma-repræsentation.
32-Bit Floating Point Number Format
Nummeret 100100.0112 kan udtrykkes som:
100100.011 2 = 1,00100011 2 x 2 +5
Højre side af =-symbolet omtales i matematik som basis to-standardformen af venstre side af 100100.011 2 .
Nu 00100011 af 1,00100011 2 på højre side af =-symbolet, uden det foregående '1'. og uden 2'eren for basen, kaldes den eksplicitte signifikand. I dette tilfælde tages det binære punkt fem steder til venstre for at have '1'. Forveksle ikke mellem decimaltegn og binært punkt. Binært punkt er for grundtal 2, mens decimaltegn er for grundtal 10. '1'. efterfulgt af 00100011 på højre side af =-symbolet, uden 2 for grundtallet, danner den sande signifikand. Dog kaldes 1,00100011 den implicitte signifikand.
Efter signifikanen i højre side er 'x 2 +5 ' udtryk. Med dette udtryk kaldes +5 for eksponenten. Plustegnet betyder, at det binære punkt skal flyttes fem steder frem for at være i sin normale oprindelige position, og 2 er grundlaget for nummereringen. Den foregående ligning kan skrives omvendt som:
1,00100011 2 x 2 +5 = 100100,011 2
Med 32-bit flydende komma-repræsentation er det '1.00100011 2 x 2 +5 ', der bruges og ikke kun '100100.011 2 ”. 2 for basen er ikke optaget. 32-bit flydende komma-repræsentation for '1.00100011 2 x 2 +5 ” tal, hvilket er lig med 36.375 10 = 100100,011 2 , er vist i følgende tabel:

Der er 32-bit positioner, som er nummereret fra højre ende, begyndende fra 0. Den første bit i venstre ende er fortegnsbitten. Hvis tallet er positivt, er denne bit 0. Hvis tallet er negativ, er denne bit 1 (-1 består af to tegn og kan ikke indsættes i en celle). Den 1.00100011 2 x 2 +5 hvilket er lig med 36.375 10 hvilket også er lig med 100100,011 2 er et positivt tal. Så den første bit er 0.
Der er otte bitpositioner for eksponenten, begyndende fra position 30 til position 23 inklusive. Den eksponent, der er skrevet der, er dog 10000100 2 hvilket er lig med 132 10 . Eksponenten for antallet af interesse er faktisk +5 af bunden af to. Så hvad sker der?
Nu, i 32-bit format, skrives en eksponent på 0 som 01111111 2 hvilket er lig med 127 10 . +5 10 er +101 2 . Så ved at nå frem til 10000100 2 i eksponentdelen i tabellen, 101 2 blev tilføjet til 01111111 2 , tilsvarende. Det betyder, at 5 blev tilføjet til 127 for at have 132 10 .
Signifikanden uden “1.” tog positionerne 22 ned til 15 inklusive. Bemærk, at 1 af '1.' er ikke angivet i 32-bit strengen. Det er aldrig angivet – accepter det. Resten af cellerne ned til position 0 er fyldt med nuller.
Hvis den faktiske eksponent er -5, trækkes 5 fra 127 10 at have 122 10 . Dette svarer til at trække 101 fra 2 fra 01111111 2 at have 01111010 2 .
Med alle de foregående illustrationer er tallet +1, som er lig med 1,0 x 2 0 = 1,0 x 1 = 1,0 er repræsenteret som:

Bemærk, at '1.' på 1,0 x 2 0 er ikke angivet i formatet. Det er aldrig angivet. Den næste blandede fraktion, der går positivt efter 1,0 er:

Læg mærke til 1'eren i højre ende. Denne repræsentation er tallet:

Forskellen mellem 1,0000001192092896 og 1,0 er:
1,0000001192092896 – 1,0 = 0,0000001192092896
Tallene med decimaldele er blandede brøker. Ikke alle brøkerne mellem 1 10 og 2 10 kan repræsenteres i computeren. Det kan antages, at det mindste brøkgab mellem de på hinanden følgende blandede tal med 32-bit flydende kommaformat er 0,0000001192092896. Forvent, at intervallet for dobbelt præcision er mindre. Se den følgende illustration.
Ved at repræsentere tallet følger 0,0 ikke de foregående argumenter. Repræsentationen for 0,0 er deklareret og skal læres som sådan. For at repræsentere 0,0 er alle cellerne for signifikanden 0, og alle cellerne for eksponenten er også nul. Fortegnsbitten kan være 0 eller 1. Desværre giver dette anledning til positiv 0 og negativ 0 som følger:

I det virkelige liv er der kun ét nul. Positive 0 og negative 0 eksisterer ikke. Dog betragtes 0 normalt som positivt. Positive 0 og negative 0 findes her på grund af denne særlige formatbeskrivelse. Tallinjen (se ovenfor) kan også have +0 og -0, men der findes kun ét nul.
64-Bit Floating Point Number Format
64-bit flydende komma-format ligner 32-bit-formatet, men med følgende forskelle:
- Der er 64 bit til at repræsentere et tal.
- Efter fortegnsbitten er der 11 bit til eksponenttallet.
- Eksponenttallet for nulindeks (2 0 ) er 1023 10 = 01111111111 2 .
- De elleve bit er efterfulgt af 52 bit for den eksplicitte signifikand.
- Det har en bredere række af tal end 32-bit formatet.
Bemærk, at '1.' det er i begyndelsen af significand er stadig ikke inkluderet blandt de 64 bit, ligesom det ikke er inkluderet blandt de 32 bit for 32-bit format.
En af de vigtigste forskelle mellem 64-bit formatet og 32-bit formatet er, at forskellen mellem de på hinanden følgende blandede fraktioner i 64-bit formatet er mindre end 32-bit formatet.
I 64-bit formatet kan intervallet (gabet) mellem 1,0 og den næste blandede fraktion beregnes som følger:
1,0 er
0 01111111111 000000000000000000000 00000000000 00000000000000000000000 2
Dette svarer til '1', som ikke er angivet i strengen, ganget med 2 hævet til potensen (indeks) 0 (med eksponenten 1023 10 = 01111111111 2 for 2 0 = 1). Snoren er 1,0 x 2 0 .
Den næste blandede fraktion større end 1,0 er:
0 01111111111 000000000000000000000 00000000000 00000000000000000000001 2
Dette svarer til '1'. som ikke er angivet i strengen, efterfulgt af 51 nuller, og derefter 1, ganget med 2 hævet til potensen 0 (hvor eksponenten er 1023 10 = 011111111112 2 for 2 0 = 1). Dette er det samme som:
+2 0 × (1 + 2− -52 ) ≈ 1,00000000000000002
≈ betyder omtrent lig med.
Nu:
1,00000000000000002 – 1,0 ≈ 0,00000000000000002
Den tilsvarende intervalværdi for et 32-bit format er 0,0000001192092896 ≈ 0,00000012.
0,0000000000000002 er meget mindre end 0,00000012. Så der er langt flere blandede brøker mellem to på hinanden følgende heltal (f.eks. 3 og 4) i 64-bit formatet, end der er mellem to på hinanden følgende heltal for 32-bit formatet.
Antallet af blandede brøker mellem to på hinanden følgende heltal på tallinjen er uendeligt. Så intet format (f.eks. 32-bit eller 64-bit) kan give alle de blandede brøker mellem to på hinanden følgende heltal (heltal). Jo mindre mellemrummet (intervallet) mellem to på hinanden følgende heltal tilvejebragt af et format (f.eks. 32-bit eller 64-bit), jo større er antallet af blandede brøker mellem de på hinanden følgende heltal (for tallinjen).
Årsagerne til, at 64-bit formatet beskrives som dobbelt eller højere præcision sammenlignet med 32-bit formatet, er, at intervallet mellem to på hinanden følgende blandede brøker afgrænset af to på hinanden følgende heltal for 64-bit formatet er mindre end de tilsvarende 32 -bit format interval. Der er også flere mulige blandede brøker mellem to afgrænsede heltal for 64-bit formatet, end der er tilsvarende for 32-bit formatet.
Konvertering af en decimaldel (brøk) af decimaltal til en binær del
36.375 er et decimaltal med decimaldelen '.375'. Decimaldelen af '.375' er en brøkdel mellem nul og en. 0,5 i base ti er den samme i værdi som 1/2 i base to. Den 0,5 10 der udtrykkes med basis to-udvidelsen er:
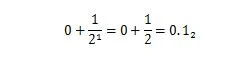
Det er ikke 0,101 2 hvilket betyder 0,625 10 . Decimaldelen af et decimaltal har sin tilsvarende binære del for det tilsvarende binære tal. Så for at konvertere et decimaltal som 36,375 10 for at basere to, konverter 36 til binær og konverter derefter .375 også til binær. Foren derefter begge resultater med det binære punkt. Metoderne til at konvertere de to sektioner er forskellige. Hvordan man konverterer et decimaltal til grundtal 2 er forklaret i kapitel 1.
Følg følgende trin for at konvertere decimalbrøken til binær brøk:
- Multiplicer decimalbrøken (decimaldelen) med 2. Det heltal, der er resultatet af dette, er det første binære ciffer.
- Gentag det forrige trin med brøkdecimalresultatet for at få det næste binære ciffer.
- Fortsæt med at gentage det foregående trin, indtil decimalbrøkresultatet er 0,0000—.
Eksempel: Konverter brøkdelen af 36,375 10 til den tilsvarende brøkdel i base to.
Løsning:
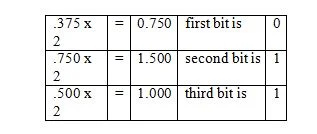
Bemærk, at i det tredje trin blev .500 ganget med 2 og ikke 1.500. Den binære tilsvarende fraktion aflæses i den sidste kolonne fra toppen. Og så er følgende resultat:
.375 10 = .011 2
Konvertering af en binær del (brøk) af binært tal til en decimaldel
For at opnå dette skal du udvide den binære brøk i gensidige potenser på 2.
Eksempel: Konverter brøkdelen af 100100,011 2 til den tilsvarende brøkdel i basis ti.
Løsning:
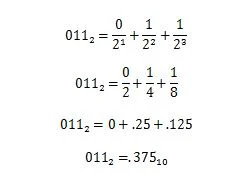
3.10 Talpræfikser i computing
I normal levetid betyder 1 kilo 1000 som forkortes i k (små bogstaver) som i 1 kg. I databehandling betyder 1 kilo 2 10 = 1024, men forkortes i K (store bogstaver) som i 1Kbits. I det normale liv betyder 1 mega 1.000.000, som er forkortet i M (store bogstaver) som i 1Mg. I databehandling betyder 1 mega 2 tyve = 1.048.576 = 2 10 x 2 10 = 1024 x 1024 = 1.048.576 og er stadig forkortet i M (store bogstaver) som i 1Mbits. I det normale liv betyder 1 giga, at 1.000.000.000 er forkortet i G (store bogstaver) som i 1Gg. I databehandling betyder 1 giga 2 30 = 1.073.741.824 = 2 10 x 2 10 x 2 10 = 1024 x 1024 x 1024 = 1.073.741.824 og forkortes stadig i G (store bogstaver) som i 1Gbits. Følgende tabel giver betydningen af fire præfikser i det normale liv og i computere:
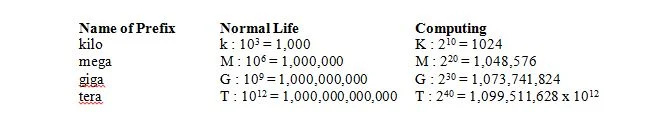
3.11 Problemer
Læseren rådes til at løse alle problemerne i et kapitel, før de går videre til næste kapitel.
- Tegn en tallinje med heltal fra -10 til +10.
- Tilføj følgende binære tal i 8-bit to-komplement: 101010 2 og 1111 2 .
- Brug kun to-komplementmetoden i 8-bit til at trække det binære tal 1111 fra 2 fra det binære tal 101010 2 .
- Find produktet af 10110 2 x 1101 2 i base to.
- Del 36.375 10 med 1000 10 i decimal og i binær, og sammenlign resultaterne.
- Brug de 8-bits efter eget valg til at illustrere de logiske AND, OR, XOR, Invert, Shift Right, Shift Left, Rotate Right og Rotate Left. Hver byte skal have en blanding af 1'er og 0'er.
- a) Skriv den numeriske kode for ASCII-tegnet nul i hexadecimal, binær og decimal.
b) Skriv den numeriske kode for ASCII-tegnet '1' i hexadecimal, binær og decimal.
c) Skriv den numeriske kode for ASCII-tegnet af 'A' i hexadecimal, binær og decimal.
d) Skriv den numeriske kode for ASCII-tegnet af 'a' i hexadecimal, binær og decimal. - Konverter 49,49 10 ind i base to. Konverter dit resultat til IEEE 32-bit flydende komma-format.
- a) Hvordan adskiller IEEE 64-bit flydende komma-formatet sig fra 32-bit-formatet?
b) Giv de to relaterede grunde til, hvorfor 64-bit formatet beskrives som dobbelt eller højere præcision i forhold til
32-bit format.